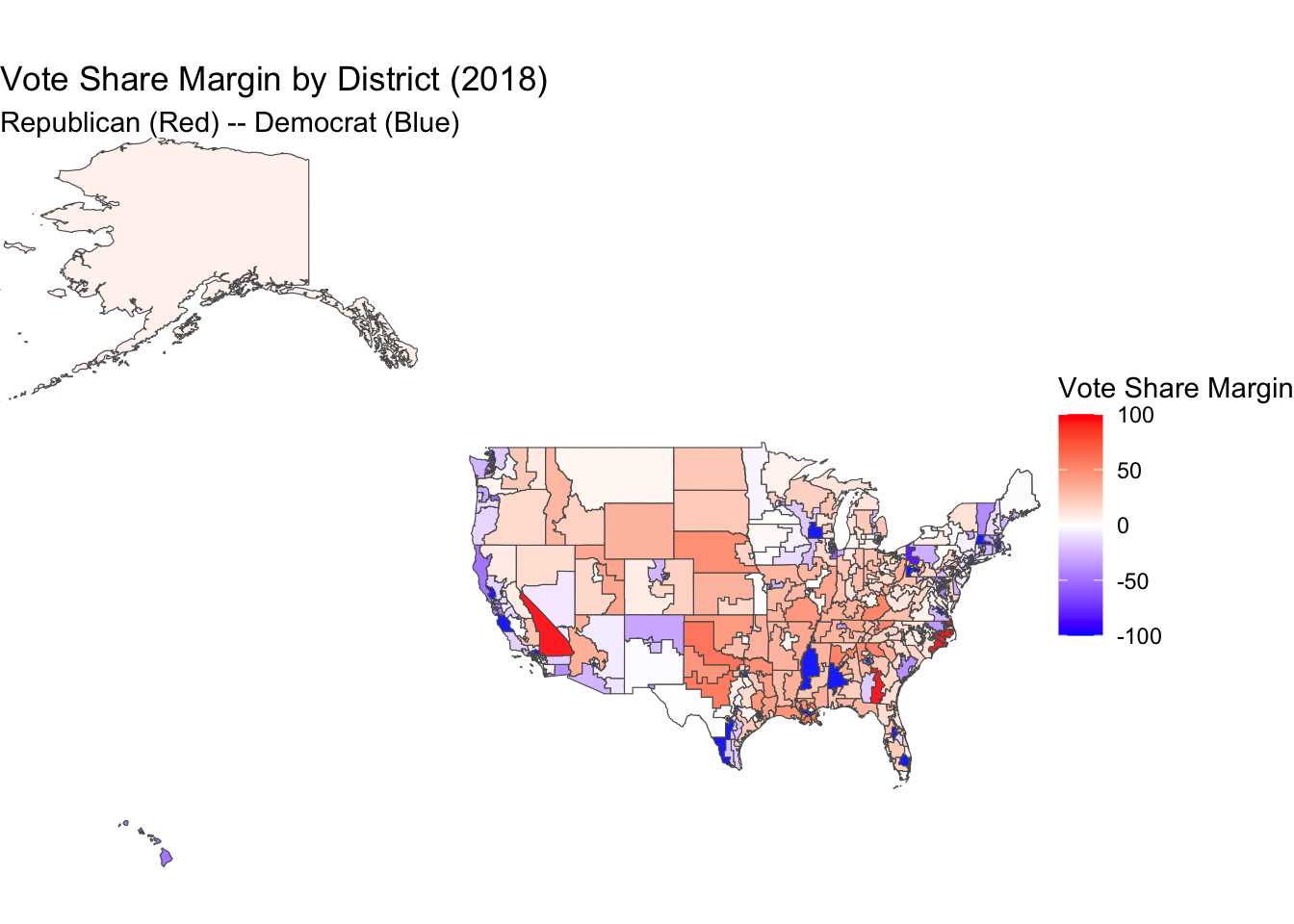
on
Week 4: Expert Ratings
This week, I looked at the role of expert rankings at a district level. This is an extension to last week’s focus on polling and incorporating variables into my model that have credibility from others in the election predicting sphere. The questions that directed my research this week were: how accurate are expert rankings, how can expert rankings be compared to actual vote share, and what does this comparison look like at a district level?
Data and Steps
This week I looked at three data sets. The first set looked at party vote share on the distinct level. This data allowed me to create a vote share margin variable between republicans and democrats. The second set looked at expert rankings from various sites for each district. The significant variable in this st is average rankings, which takes the average of the rankings on a scale of 1-7 (Solid D to Solid R). Finally, I looked at incumbency data for each district. This shows if the incumbent or challenger won for that district. For all data, I looked at the most recent midterm, filtering the data to 2018.
Mapping Expert Rankings
The map below shows the expert rankings for each state on a scale of 1 to 7 (Solid D to Solid R). This map follows a fairly similar trend as the actual vote share. To more directly see the relationship between expert rankings and vote share, I converted the rankings to vote share in the following map.
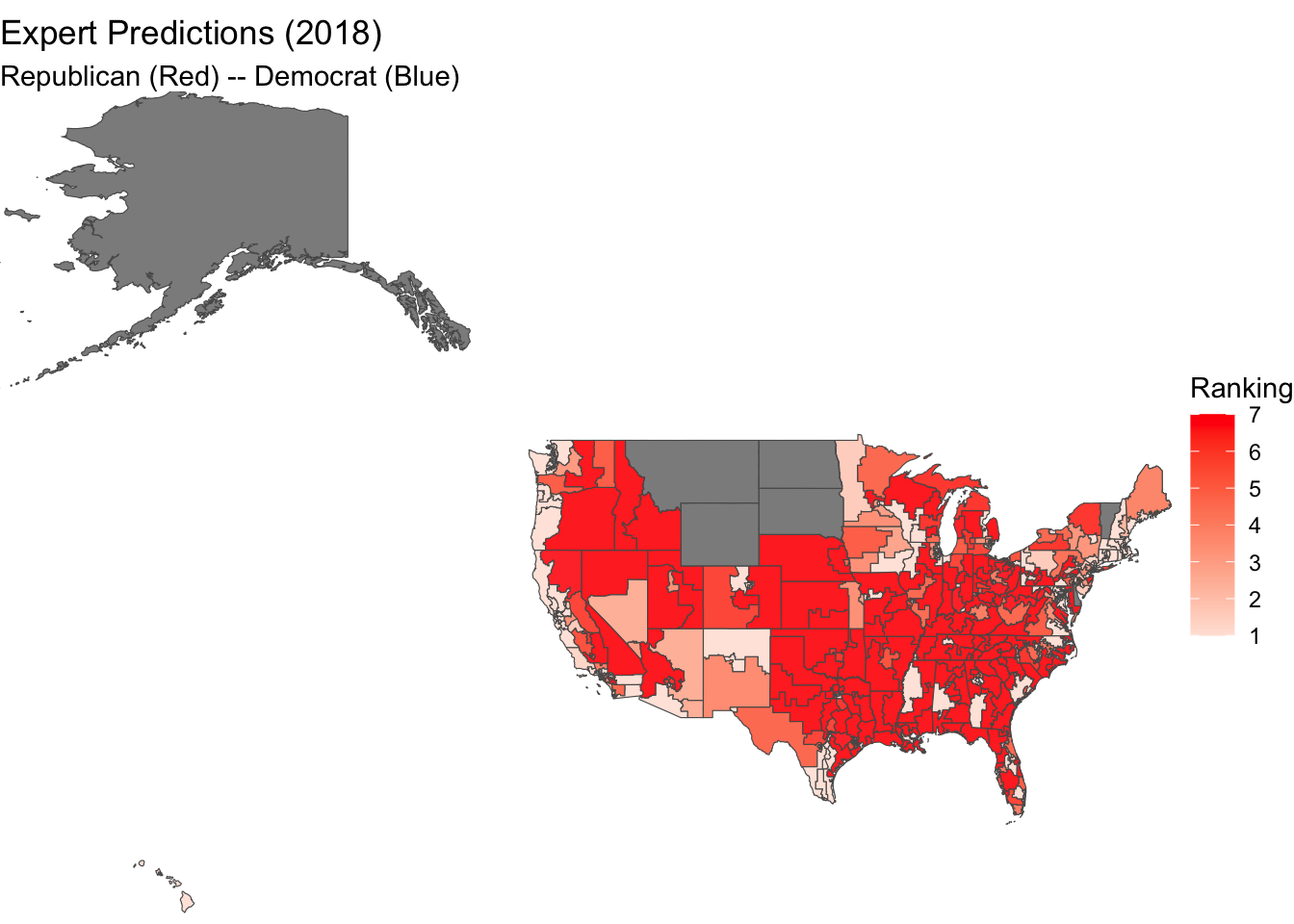
Mapping Difference Between Actual Vote and Expert Ranking
For this map, I converted the seven categories into a related vote share for democrats: Solid D = 60 Likely D = 55 Lean D = 52.5 Toss up = 50 Lean R = 47.5 Likely R = 45 Solid R = 40
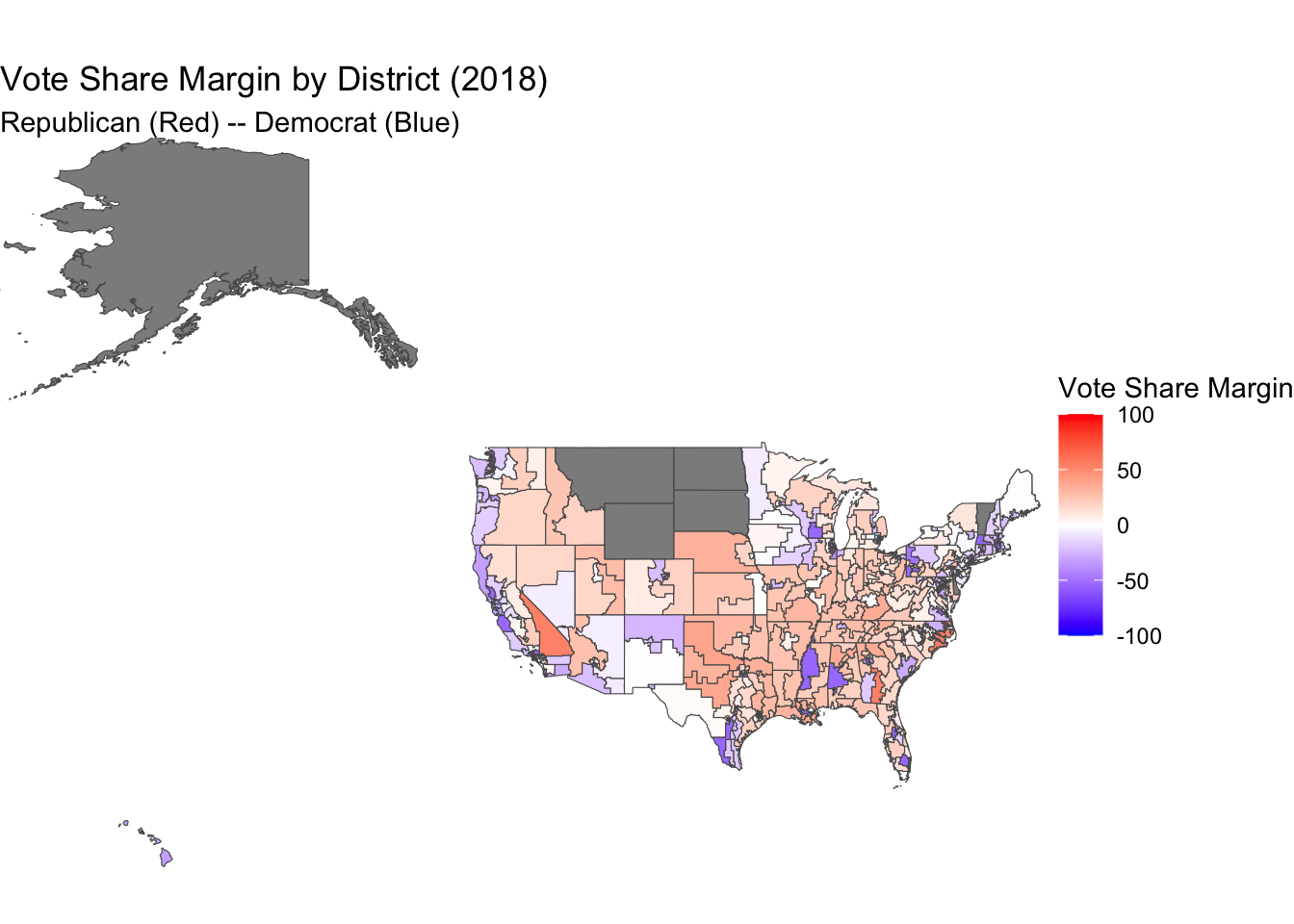 # Analysis
# Analysis
Looking at these three maps, all three follow the same general trends across the country. One of the most significant disparities is with how unchallenged candidates impact the vote share. For example, in New York’s 16th district, there was a 100% democratic vote share. This is because the democratic candidate ran unopposed and therefore there were no republican votes. However, in the expert rankings map, this would only register as a Solid D and therefore only get 60% of the votes. By hardcoding these values in it makes it difficult to measure and map the validity of expert rankings to the actual vote share of the district.
Model Updates
This week, I also formalized my model from the collection of variables analyzed the past few weeks. After looking at economic fundamentals in week 2, I decided to add another variable, CPI, which proved to be the strongest predictor of vote share compared to GDP, RDI, and unemployment. In week 2, I also noticed that economic predictors appeared strongest in Q7. For this reason, I used CPI from October of the election year in my model (Healy and Lenz). In week 3, I looked at polling averages. I found that polling was strongest the month prior to the election, so filtered for polls from October to the election. In this model, my predicted Republican Vote share is 48.21% and my predicted Democratic vote share is 49.95%. These values use the most recent generic ballot polls. However, for both of these values, my adjusted R-squared is about 0.2 which is very low, and indicates that these predictions do not hold much statistical significance.
## New names:
## Rows: 3284 Columns: 23
## ── Column specification
## ──────────────────────────────────────────────────────── Delimiter: "," chr
## (2): party, winner_party dbl (21): ...1, ...2, year, quarter_cycle,
## GDP_growth_qt, DSPIC_change_pct, ...
## ℹ Use `spec()` to retrieve the full column specification for this data. ℹ
## Specify the column types or set `show_col_types = FALSE` to quiet this message.
## • `` -> `...1`
## • `...1` -> `...2`Moving Forward
After looking at expert ratings at the district level, this data will help me construct a district level seat share model. However, I will not be creating a district level model this week as expert ratings would be the only variable I could add, making for a poor model. Although, I will also consider adding a variable around incumbency in my model.